Zwar kennen wir jetzt die Preiseinflussgrößen und wir wissen auch, wie sich Veränderungen der einzelnen Faktoren auf den Optionswert auswirken. Doch das reicht noch nicht, um den Kurs auf Mark und Pfennig genau bestimmen zu können. Wir müssen noch wissen, wie man die Einflussfaktoren miteinander verknüpfen muss, oder anders gesagt fehlt uns die Formel, in die man die Werte für die Preisfaktoren einsetzen und dann den Optionspreis ausrechnen kann. Eine solche Formel haben – wir erwähnten es zu Beginn dieses Artikels – die Amerikaner Black und Scholes entwickelt. Auf die Herleitung verzichten wir. Ebenso ersparen wir uns den Abdruck der Formel, denn inzwischen werden Optionsrechner angeboten und deshalb muss man die mathematische Struktur der Formel nicht kennen. Anwender ist lediglich gezwungen, die Werte für die Preisfaktoren zu beschaffen und einzugeben. Dennoch sollte jeder Optionsanleger wissen, auf welchem Prinzip die Formel von Black/Scholes basiert. Unter bestimmten Voraussetzungen, auf die wir hier aber nicht näher eingehen, lässt sich die (geschätzte) Volatilität in Wahrscheinlichkeiten umwandeln. An der Vola kann man also ablesen, wie groß die Wahrscheinlichkeit ist, dass zum Beispiel die T-Aktie in einem Jahr zum Börsenkurs von 100 Euro, 105 Euro oder irgendeinem höheren oder niedrigeren Kurs notiert. Nehmen wir zur Veranschaulichung zwei Aktien A und B. Der Kurs von A soll in einem Jahr mit einer Wahrscheinlichkeit von 30 % bei 80 Euro, mit 40% bei 100 Euro und schließlich mit einer Wahrscheinlichkeit von 30% bei 120 Euro liegen. Aktie B hat eine etwas andere Verteilung. Damit deutlich wird, wie die Wahrscheinlichkeiten mit der Volatilität Zusammenhängen, haben wir die Aktienkurse und ihre Wahrscheinlichkeiten – getrennt, für A und B – grafisch dargestellt. Man kann erkennen, dass die Schwankungsbreite der Aktienkurse bei B stärker ausgeprägt ist als bei A.
| Kurs der Aktie B in einem Jahr | Wahrscheinlichkeit |
| 60 Euro | 10% |
| SO Euro | 20% |
| 11>0 Euro | 40% |
| 120 Euro | 20% |
| 140 Euro | 10% |
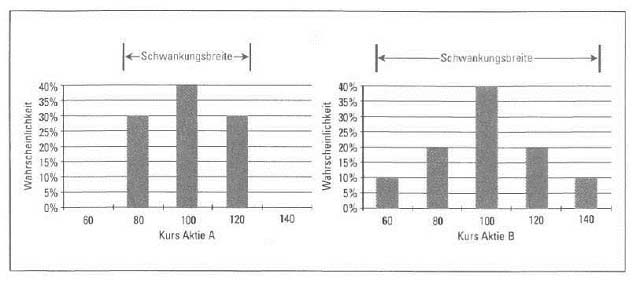
Aus den Verteilungen der Aktienkurse kann man nun herleiten, mit welcher Wahrscheinlichkeit ein bestimmter Innerer Wert am Ende der Laufzeit auftritt. Am Fall einer Call-Option wollen wir das einmal demonstrieren. Am Verfalltag hat der Call nur dann einen Wert (Inneren Wert), wenn der Kurs der A-Aktie den Basispreis überschreitet. In 30 Prozent aller Fälle notiert A /um Kurs von 80 Euro, in 40 Prozent der Fälle hat die Aktie einen Kurs von 100 Euro. Das bedeutet, dass die Option in 70 von 100 Fällen am Ende der Laufzeit wertlos verfällt. Mit 30-prozentiger Wahrscheinlichkeit notiert A in einem Jahr zum Kurs von 120 Euro. Dann besitzt der Call einen Wert von 20 Euro. Für die Optionswerte erhalten wir deshalb die Wahrscheinlichkeiten in der Tabelle. Nun stellt sich folgende Frage: Welchen Wert darf ein Finanzprodukt haben, das in 70 Prozent der Fälle wertlos ausläuft und in den restlichen 30 Prozent einen Rückfluss von 20 Euro einbringt? Angemessen wäre ein Preis, der dem gewogenen Durchschnittswert entspricht.
| Cali-Option | |
| Underlying | Aktie A |
| Strike Price | 100 Euro |
| Laufzeit | 1 Jahr |
| Andienung | Barausgleich |
| Ausübung | amerikanisch |
| Innerer | Wahrscheinlichkeit |
| Wert | |
| 0 Euro | 70% |
| 20 Euro | 30% |
Gewogener Kursdurchschnitt: 70 x 0 Euro + 30 x 20 Euro/100= 6€
Warum sind 6 Euro ein fairer Preis? Angenommen, wir würden hundertmal nacheinander die Option kaufen und jedes Mal 6 Euro dafür bezahlen. Insgesamt hätten wir dann 600 Euro investiert. In siebzig Fällen wäre unser Kapitaleinsatz verloren, in dreißig Fallen fließen jeweils 20 Euro an uns zurück, insgesamt also 600 Euro. Wir hätten im Ganzen betrachtet weder Gewinn noch Verlust erzielt. Als Käufer können wir den Optionspreis deshalb durchaus akzeptieren. Doch ist der Wert auch für den Stillhalter akzeptabel? Für einhundert verkaufte Optionen erzielt er einen Erlös von zusammen 600 Euro. In siebzig Fällen verfallt das Kaufrecht wertlos – der Stillhalter wird nicht in Anspruch genommen. Dagegen ist er in 30 Prozent aller Fälle zu einer Auszahlung von 20 Euro verpflichtet — 30 Zahlungen ä 20 Euro machen insgesamt 600 Euro. Genau wie der Käufer gibt der Stillhalter letztlich so viel wieder aus, wie er eingenommen hat. Es entsteht weder Gewinn noch Verlust. Damit man sieht, wie die Volatilität den Optionspreis beeinflusst, tauschen wir bei unserer Kaufoption nun .Aktie A gegen B aus. Damit ändert sich die Situation wie in nebenstehender Tabelle gezeigt wird. Die Wahrscheinlichkeit, dass die Option in einem Jahr wertlos verfällt, liegt weiterhin bei 70%. Im Vergleich zur Aktie A besteht nun allerdings die Chance, dass Kurse von 140 Euro erreicht werden. In zehn von hundert Fällen ist der -Call am Verfalltag 40 € wert, in zwanzig Fällen fließen 20 Euro an den Inhaber zurück. Der Durchschnittswert liegt deshalb bei 8 Euro. Die höhere Volatilität führt zu einem um 2 Euro höheren Optionspreis.
Gewogener Kursdurchschnitt: 70 x 0 Euro + 20 x 20 Euro -H 10 x 40 Euro/100 = 8 Euro Damit haben wir grob beschrieben, auf welchem Prinzip die Methode von Black und Scholes basiert. In vielerlei Hinsicht sind die
| Kurs der Aktie 8 irr einem Jahr | Innerer Wert des Call | Wahrscheinlichkeit |
| 60 Euro | 0 Euro | 10% |
| 80 Euro | 0 Euro | 20% |
| 100 Euro | 0 Euro | 40% |
| 120 Euro | 20 Euro | 20% |
| 140 Euro | 40 Euro | 10% |
Fallbeispiele stark vereinfacht, so ist etwa die Wahrscheinlichkeitsverteilung in der Realität: erheblich feiner abgestuft. An unseren Fallbeispielen kennen wir jedoch erkennen, dass sich der Wert einer Option im Wesentlichen auf die Merkmale des Underlyings zurückführen lässt, insbesondere dessen Preis und Volatilität. Deshalb zählt man Optionen – wie wir im ersten Teil schon erwähnten – zu den derivativen Finanzinstrumenten (kurz: Derivate).
 Geld Anlegen 24h Ihr Geld Richtig und Sicher Anlegen
Geld Anlegen 24h Ihr Geld Richtig und Sicher Anlegen



